How To Find A Constant In A Function

Previously y'all learned about functions, graph of functions. In this lesson, yous will learn most some function types such as increasing functions, decreasing functions and constant functions. These concepts are explained with examples and graphs of the specific functions where ever necessary.

Increasing, Decreasing and Constant Functions

Functions are increasing, decreasing and constant when you lot plot the graph of the function in a coordinate system. Allow'south define the pregnant of these functions.

Increasing function

A office $f(x)$ is increasing in an interval for any $x_1$ and $x_2$

Case:

Let $f(x) = x^2 + 1$ be a function. Notice all the values for the office to plot the graph.

ten	f(x)	(x, f(10))
-1	ii	(-ane, 2)
0	1	(0, 1)
i	ii	(1, 2)
two	5	(2, v)

The graph of the role will look like the following.

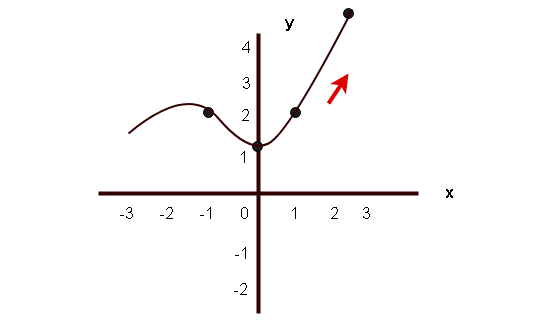
In the above graph, the function is increasing between the interval of (0, 2).

The value of $x_1$ is 0 and $x_2$ is 3,

The value of $f(x_1)$ is 1 and $f(x_2)$ is five.

Therefore,

$x1 < x2$ implies $f(x_1) < f(x_2)$ is true and information technology is an increasing office.

Decreasing Function

A function $f(x)$ is decreasing in an interval for whatsoever $x_1$ and $x_2$

Example:

Consider a function $f(x) = x^2$ . The part is a parabola. Let's draw the graph of this function in a Cartesian plane or co-ordinate system.

Before plotting the graph, you demand to find points for the graph of the function. A tabular array of points is given below.

x	f(10)	(x, f(x)
-2	4	(-2, 4)
-1	i	(-1, 1)
0	0	(0, 0)
1	1	(one, i)
2	four	(2, iv)

The graph of the parabola is given beneath.

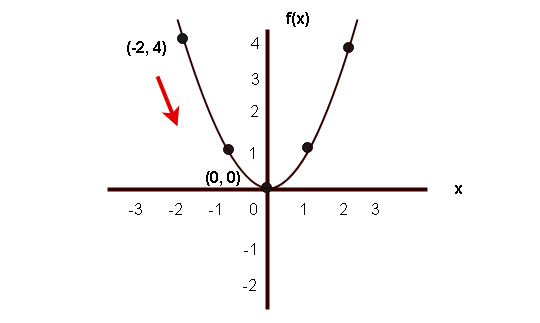
In the above graph, the part is decreasing between the interval ( -2, 0).

The value of $x_1$ is -2 and the value of $x_2$ is 0.

The value of $f(x_1)$ is 4 and the value of $f(x_2)$ is 0.

Then

$x_1 < x_2$ is true and $f(x_1) > f(x_2)$ is likewise true. Hence, the function is a decreasing role between the interval $(-2, 0)$ .

Constant Part

The part is a constant office in an interval for some $x_1$ and $x_2$

This is simplest form of graph of a role and such a function is always a straight line on the coordinate arrangement.

Let $f(x) = 3$ be the constant function. It means for whatsoever value of $x$ in the domain, the value of $f(x)$ is 3.

The graph of abiding part is given beneath.

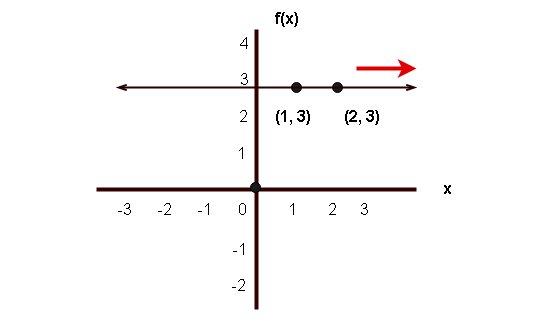
In the to a higher place graph of the constant function.

The value of $x_1$ is one and the value of $x_2$ is 2.

The value of $f(x_1)$ is three and the value of $x_2$ is also three.

Therefore,

$x_1 < x_2$ and $f(x_1) = f(x_2)$ implies that the function is a constant function.

Related Articles:

Cartesian Plane
Graph of Equations
Functions
Graph of Functions

Source: https://notesformsc.org/increasing-decreasing-constant-functions/

Posted by: hiersmorgilizeed.blogspot.com

How To Find A Constant In A Function

Increasing, Decreasing and Constant Functions

0 Response to "How To Find A Constant In A Function"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel